ShoelessCai - 杭州值得 | 支持向量机 SVM 的“应试记忆法”

杭州值得 | 支持向量机 SVM 的“应试记忆法”

- 2024 -
08/20
16:13

零号员工

发表时间：2024.08.20 作者：Jingyi 来源：ShoelessCai 阅读：127

原标题：支持向量机 SVM 的“应试记忆法”

此前写过一些 SVM 的问题，点击阅读《SVM、SMO 算法代码解析》。

首次遇到这个算法是吴恩达的《Machine Learning》，Coursera 非常有名的先上课。应用方面，例如，垃圾邮件分类，这类二分类问题。

解释这个算法，Intuitive 的解释是，找到超平面，分割两个“簇”的点。因为簇之间实际的间距有大有小，还有个“灰带区间” —— 软间隔的概念。

今天再来巩固一下吧。

01 SVM Primary Problem 原问题

两个关键点：第一，权重的平方和最小。第二，权重对应的线性平面，使得该平面与点的距离之和大于某个阈值。注意，原问题和对偶问题的表达式，都来自于周志华老师的《机器学习》。

02 SVM Dual Problem 对偶问题

如图所示，对偶问题解决的问题是，无论原问题是否是凸的，对偶问题永远都是一个“凸优化问题”，且只有一个待定系数 α。

这个问题关键，系数与平面是垂直的！

03 KKT 条件

我们想要用对偶问题代替原问题，就需要这个不等号取等。对于拉格朗日方程取等的条件，数学家们已经有了严谨的证明，只需要满足Karush-Kuhn-Tucker条件（简称KTT条件）。

KKT 存在的意义是，使得对偶问题，min_x(max_αβ(L)) …… （1）

和对调这个 min() 和 max()，即 max_α(min_x(L)) …… （2）

当且仅当 (1)=(2)，可以通过解决对偶问题，来解决原问题。问题来了 —— 怎么保证这个等号是相等的呢？

答案是，满足 KKT 条件。

我们参考的博客园《深入理解SVM，软间隔与对偶问题》，这篇文章说到，暂时理解为：满足 KKT，就可以使得 max_α(min_x(L)) = min_x(max_αβ(L))，于是，我们可以直接解决对偶问题。对偶问题的优势之前也说过，这里再强调，SVM 对偶问题永远都是凸的，总归能找到最优点。

关于 KKT 条件推导，基本思想是用拉格朗日乘子法解决最优化问题，对每个变量、我们加的参数求偏导之后，获得的方程组，则为 KKT 条件。

周志华老师《机器学习》对 KKT 条件的刻画。

作为最优化领域里比较有名的约束条件，肯定是要记住的！

口诀：第一，系数恒正。第二，系数垂直于样本点张成的平面。第三，样本点处于平面的一边，大于 1（因为是分割两个簇）。

04 软间隔

这里先复习【支持向量】的概念。

我们都知道支持向量选得不一样，平面会随之变动。相应地，核函数选定得不一样，则“平面”形态会不一样。点击阅读《机器学习（周志华）课后习题——第六章——支持向量机》，获得更多信息。

平面，是训练出的系数 α 决定的。

间隔，即【支持向量】（某几个样本点）到α- 平面之间的距离。

接下来解释“软间隔”。

第一，“软间隔”，必然和“线性不可分”一起出现。换言之，“线性不可分”问题中，总有样本点，无法用线性的方法分干净，此时引入“软间隔”概念。

第二，“软”意味着“弹性”，软间隔内，允许部分样本点分类错误。对应分隔区间内没有任何分错的样本，称为“硬间隔”。

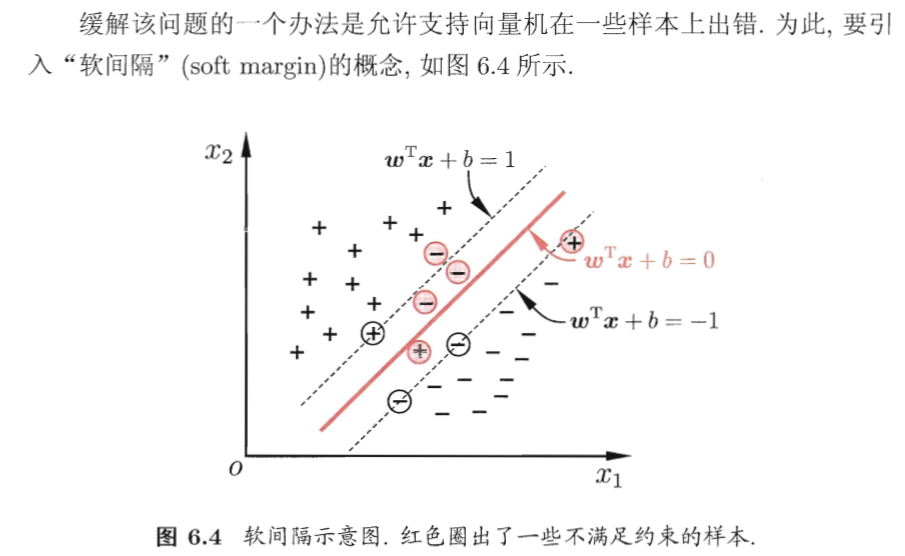
“软间隔”允许判错多少个样本？

这是个好问题，笔者查阅了周志华老师的书之后，这么解释。

首先，这是个最优化问题。

其次，但凡最优化问题，众所周知，不是使得某些点没作用，而是用数学方法，使得某些点尽量作用减到最小。于是引入“松弛变量”。

于是，这样可以比较好地解释“软间隔”应用，即引入一个概念描述一种情况，然后基于这个范畴之下，解决这个实际问题。基本思想，不是这个间隔里容纳多少错误，而是“因地制宜”地使得每个最优化问题在软间隔里犯的错最少，同时目标函数 Loss 尽量最少。计算通常由计算机完成，这整个过程，称为“软间隔支持向量机”。

“软间隔”物理意义

首先，我们考察带有“松弛变量”的最优化对偶问题，是不是形态和原来很像，只不过在系数 α 的约束上，多了一个常数 C。这物理含义就是，α这个向量，已经无法“自由”地和所求平面垂直了。

然而，大多数的实际问题，就是满足这种“垂直”假设的。不然要找到最优解，也太容易了吧？对吧？

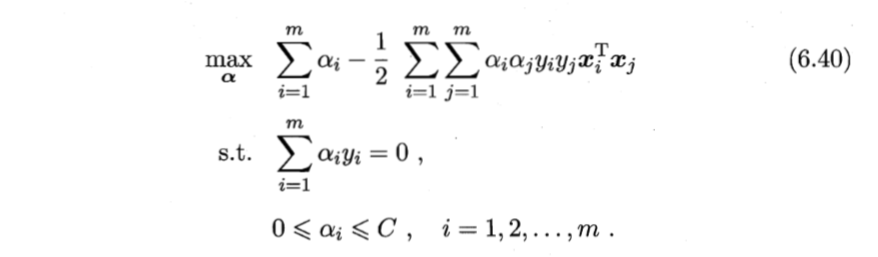
更一般地，我们把现实中试图要解决的问题下称如下形式。

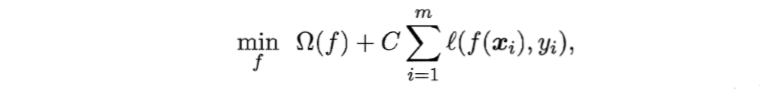
左边是“结构风险”，来自于权重的分布；右边是“经验风险”，来自于回归出来的结果。这是一种便于记忆的公式。

05 应用

应用方面，我们参考这篇文章，写得蛮清楚的。作为二次文献，笔者取所需，再写点注释。点击阅读《基于SKLearn的SVM模型垃圾邮件分类——代码实现及优化》，获得更多信息。

第一，先从特征提取开始吧，我们的目标是将一整句句子，变成若干个单词向量。当一篇文献进入的时候，系统自动统计该文献内的某个词汇，出现了多少次。如图所示。

代码如下。

1 def textToMatrix(text):
2 cv = CountVectorizer()
3 cv.fit(text)
4 vocabulary = cv.vocabulary_
5 vector = cv.transform(text)
6 result = pd.DataFrame(vector.toarray())
7 del(vector) # 及时删除以节省内存空间
8 features = []# 储存特征值
9 for key, value in vocabulary.items(): # key, value 示例 '孔子'， 23772 即词汇,字符串的形式
10 if result[value].sum() >= THRESHOLD:
11 features.append(key) # 加入词汇表
12 result.rename(columns={value:key}, inplace=True) # 本来的列名是索引值value，现在改成key ('孔子'、'后人'、'家乡' ..等词汇)
13 return result[features] # 缩减特征矩阵规模，仅将特征词汇表中的列留下

最上方为 “特征词汇”，之后的每一行数据代表一封 Email （也称文献）的内容，数值代表“对应词汇在这个 Email 中的出现次数”。可以看出，SVM 不能对语句的顺序关系进行学习，不同 Email 内容可能对应着同样的特征向量结果。

例如：“我想要吃大苹果” 与 “吃苹果想要大我” 对应的特征向量是一模一样的。不过一般来讲问题不大，毕竟研表究明，汉字的序顺并不能影阅响读嘛（牛云杰，2021）。

关于训练模型，代码的基本思路。

首先，是读取正例邮件和反例邮件，并生成其对应的 label 序列，将邮件转化为由特征向量组成的 matrix。在本例中，特征词汇正好有256个，也就是说特征向量的维度为256。

原则是，保存特征词汇，使用 SVC 模块建立 SVM 模型，分离训练集与测试集，拟合训练，对测试集进行计算评分后保存模型。

1 ham_str_all = email_cut(path_list_ham)
2 spam_str_all = email_cut(path_list_spam)
3 allWord = []
4 allWord.extend(ham_str_all)
5 allWord.extend(spam_str_all)
6 labels = []#标签
7 labels.extend(np.ones(len(path_list_ham)))
8 labels.extend(np.zeros(len(path_list_spam)))
9 vector = textToMatrix(allWord) #获取特征向量
10
11 feature = list(vector.columns)
12 print('feature length:',len(feature))
13 with open('./model/CN_features.txt', 'w', encoding='UTF-8') as f:
14 s = ' '.join(feature)
15 f.write(s)
16 svm = SVC(kernel='linear', C=0.5, random_state=0)
17 # 线性核，C的值较小时 可以允许一些错误可选核：
18 # 'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'
19
20 # 将数据分成测试集和训练集
21 X_train, X_test, y_train, y_test = train_test_split(vector, labels, test_size=0.3, random_state=0)
22 svm.fit(X_train, y_train)
23 print(svm.score(X_test, y_test))
24 model = joblib.dump(svm,'./model/svm_model.m')

接着是调整和优化。

整个实践建模的过程其实到上面已经结束了，但在实际使用的过程中，发现有下面2个问题：

第一，训练速度非常慢，完全不像线性模型，接近神经网络的速度；

第二，内存消耗太大。这篇文章的原著作者训练电脑 16 GB内存，全被占满。

如何解决？

经过不停地锚点，消耗最大的是 textToMatrix() （毕竟是别人写的函数），语句

result.rename(columns={value:key}, inplace=True)

这条语句的意思是将 pd.DataFrame的某列列名进行替换，由 value 替换为 key。作者输入的样本是 40000 个，导致极大的时间开销。

解决这个问题的思路由两个：一是对列名构建索引，以便快速定位；二是重新构建一个新的 pd.DataFrame 数据表，将改名操作批量进行。评注：第二点不算很看懂，不出意外的话，是指你注销这句语句。同时，用一个 list() append 即可。

作者选择第二种思路，就是空间换时间，重写 textToMatrix()函数。我们这里是转述，就不贴出来。点击阅读《基于SKLearn的SVM模型垃圾邮件分类——代码实现及优化》，获取更多信息。

最终，仅耗时 2 分钟便完成 SVM 模型的训练，比优化代码之前速度提高了 60 倍。在测试集上的预测精度为 93.6% 的准确率，也算是比较实用了（牛云杰，2021）。