这几天复习中,脑袋中总是想起几首歌:
早知解散后,各自有,际遇作导游,奇就奇在接受了各自有路走 —— 很像三体当中的激进派和回归派。
《最佳损友》
难道你想 没什么意外 发一生的呆
墓志铭 只要写 人畜无害
还是怕输 不参加比赛 把自己淘汰
到老了 才发现 小宇宙 根本就 没打开
《Do You Ever Shine?》
我想了想,搞事情总归不算好事情,那就多参加比赛吧!好在现在有很多比赛,还能赚钱呢!艺术类的,现在有很多综艺明星会自己办比赛。
好啦,我的比赛现在拉开帷幕,我自己也在研究一些点,我也会参加一些比赛。因为,先导知识比较少,所以用 bullet point 记录,没有总结和抽象的过程。
西湖大学 2024 年 12 月 5 日 晚 7 点直播
西湖大学直播:关于强化学习
TD 算法:时序差分方法,我们姑且认为,这是强化学习一套算法里的其中一个。
 图片来源
图片来源
状态函数

按照讲师的说法,状态函数,永远都能收敛到真实函数,只要次数够 —— 量变到质变,因此速度机器重要,我这几天仿佛水下作业,速度奇慢,要加油!
点击
获取原文。
对 action 的条件限制
昨天看错了,今天改的,2024.12.7。
第一,∑a^2 < ∞,每个状态都要被访问很多次;a 是行动的意思;
第二,在实际应用中,通常 a 取 0.001 这样量级。
以上这个笔记,是用于跑模型参考的。
这是 12.7 早上修改的笔记,本来我在音频里也说,看成了学习率(或者加权的权重)α,昨天再次阅读的时候,发现是 a。我自己在做笔记的时候也没仔细看。那么,借此机会,看看 a 在实际业务中到底怎么表示的。
这篇文章《
强化学习-学习笔记15 | 连续控制 》,讲的蛮清楚的。
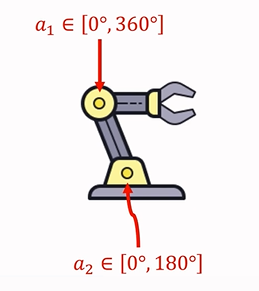
案例-I(机械臂):假设 a 表示 action 的取值,是两个角度的值,如果是二维向量,则为 [0°,360°]×[0°,180°]。
所以,针对 action,就是在上述区间内的值。
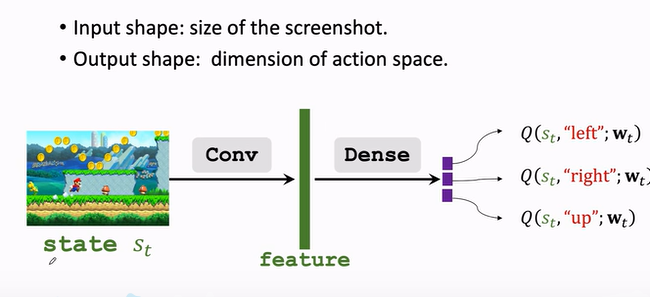
案例-II(超级马力):顺道理解一下,q 这个在公式中的值,在实际业务里怎么表示。主人公在走路的时候,每次可选的选择是 [left, right, up],对应 q 为[0.2, 0.1, 0.7]。这个值用于算之后的价值 V (upon state-t)。

时序差分 TD / Sarsa 算法
TD 算法,或者待会要讲的 Sarsa 算法,有以下特点:
第一,Online Policy,我们会发现 Offline Policy 情形不是很多;
第二,算法是连续的;
第三,Bootstrapping 方法,重复抽象,重复调试。
Sarsa 算法简介
首先,我们区分价值函数 q,以及策略函数 Pi。这句话的含义是,q 有最值,Pi 也有最值。
其次,算法两阶段,先更新所有的价值函数,然后估计所有的策略函数,然后更新策略。注意到,价值 q,依赖于你的行为 a的。暂时学到这种程度。
ε-greedy
实验是这么演进的,一个 episode 就是一个迭代,例如你迭代 500 个 episode,你就有 500 个 reward。一开始的时候,你获得的 reward 都是和真实,或者说和最佳策略差得很远的,之后 reward 会逐渐收敛到比较真实的水平。
我们把这类 greedy 探索的 PPT 放到最后了!
n-step Sarsa,这里我睡着了。
On-policy 定义:存在两种策略,behavior policy 和 target policy,两者一致,称为 On-Policy。
Off-policy 定义:behavior policy 和 target policy 不收敛。注意,Q-learning 存在 off-policy 版本。
课件
接下来放几张 PPT,我解释一下。

Sarsa 算法简介

Sarsa 算法策略迭代
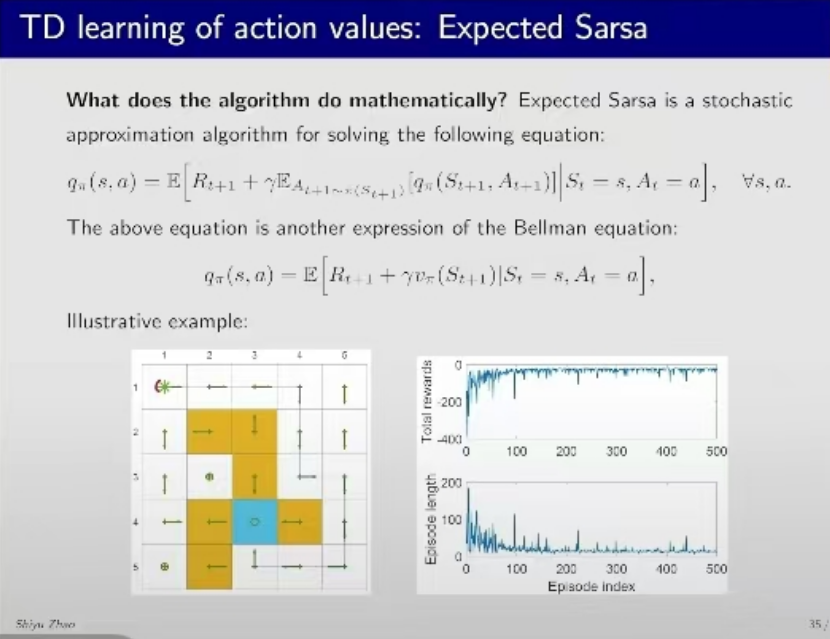
贝尔曼方程,其实我的理解是,(1)上一轮的回报,(2)上一轮模拟的最后策略回报,做一个加权平均

这是 Q-learning On-policy 部分。和 Sarsa 差异在于,Sarsa 迭代的最后一个 item,系 q(S_t+1, a_t+1)。最后一个 item 换掉之后就是 Sarsa 算法。
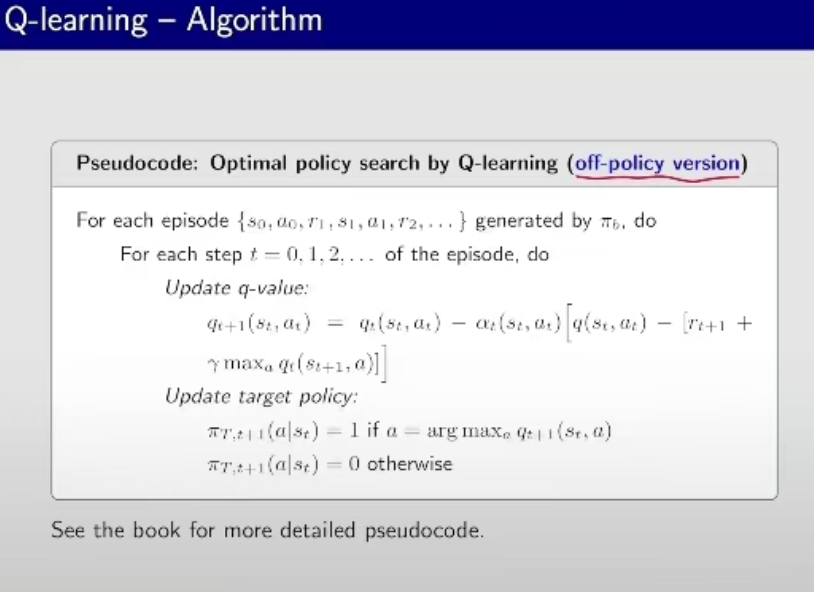
Off-policy 版本的迭代算法,暂且做参考吧。
ε-greedy Graph
以下 2 张图挺有意思,内容是 ε 取不同值的时候,收敛情况。曲线下降得越低说明,越接近真实情况。后面ε较小的时候,即以 10% 概率探索的时候,能够搜索到的比例比较少,相应的曲线也会下降得比较缓慢。

这个是较大概率探索的情况。

这个是 ε = 0.1 情况。

针对不同算法,贝尔曼方程有不同的表现形式。
