斟酌一下,说不定要不然搞个积极版的!
看完《逻辑学讲话》,自觉不算太理解,而且很没耐心啊!但是大家还是大家,书不在厚,有用则行。当时的文人学者都看阅读量,而他们的阅读量,确实也够笔者,这样的文化水平的人,去做出决策了。也不造作,所以得出结论,读书做学问还看阅读量。
因此,这里就不放太多摘抄了,在准备写读书笔记的时候,想想咱们还是写写感想。这本书很有意思,我最印象,引经据典的一句话,“穷人家按照富人家做事规则,那么其命运是必然的”。我们中国人都说穷且益坚不坠青云之志,我们也知道在商言商,“商人重利轻别离”,很多富人和自己想象中还是差异挺大的,这当中具有一个比较大的情商鸿沟,需要用努力和智力去填补。
为什么努力放在前,智力放在后呢?
因在商言商,很多事情还是功利的多,因此一个人的智力如何,很多人其实并不关心,很多人更加关心,一个人的智力如何通过动手能力转换成产品(或者商品),商品如何通过流通产生对社会的价值,价值如何和通过人与人之间的交互变现成货币。后面的逻辑链条才是人们更加关心的,任何逻辑断了的,都无法怨天尤人。
所以,笔者认为,“怀才不遇”是个贬义词。因一个人必须得有这样的基本能力,知道自己的水平和特长,这样才能有自知之明,有知人之明。至少,这是对笔者的要求,笔者对别人没有这个要求。然而,大家都清楚,团队有人要是怀才不遇的话,也是很 tough 的。
voice message —— 别被部分词汇吓跑啦!1.5倍速!
2025.8.16 还是把摘抄写了吧!!
有些书曾经畅销一时,但现在已经不容易得到;有些书当时或许没有引起很多人注意,但时间证明它们价值不菲。
人文科学则不然,有许多书是常读常新的。
在路边等人的时候,在排队买戏票的时候,在车上、在公园里,都可以读。
判定问题是数理逻辑的核心问题之一。
20世纪初,希尔伯特(D.Hilbert,1862-1943)在数学基础研究中提出形式主义纲领,致力于通过有穷多一阶公理来对各种数学分支进行公理化,原则上,这样的公理化把数学命题的证明归约为在一个指定的形式逻辑系统中执行一种机械的推导,在这样的情况下,判定问题尤其重要。
1915年,谢孚的一个摘要对于理解文稿背后的潜在动机至关重要,摘要只有一句话,即“通过各种‘关系坐标的变换’和相应的系统等价性定义,谢孚博士为包含有穷多个元素的演绎系统建立了一个一般性的公理理论”,而标题则清楚地表明,对有穷的关系系统的研究只是迈向谢孚所希望的演绎系统的一般理论的第一步。
有穷关系结构是形如
的结构,其中 K 是包含 n 个元素的有穷集合,R 是定义在 K 上的 m 元关系。
令 F 是如下这样一个结构族,它对于 K = {1,…, n} 上所有置换的对称群 Sym(K) 是封闭的,也就是说,如果 a 是 K 的一个置换并且〈K,R) 在 F 中,那么 くK,R> a 也在 F 中。
结构 组成的族是范畴的,仅当这个族中的所有结构都是同构的。
这些结果阐明了对元素结构“格栅”(graf),成立的定理:取一个有序元素的二维网格并排列这些元素,在格栅的组合重排下,看看哪些“形式”和“关系”相对于基数和其他高阶属性仍然是正确的。
评注,作者部分文章在报刊上发表,当时具有比较强的思辨性质。关于“超公理”的论证,是否存在超公理,使得其足够 general,使得其覆盖到所有公理。作者认为是存在的,而且事实上,这些公理的集合“不变量”具有非常简单的性质。
我们假设有一个算法来确定一个公理集合的不变量;这个假设似乎是合理的,因为谢孚说不变量有“一个非常简单的特征”。根据这个假设,谢孚声称他有一个算法来确定两个一阶公理系统是否等价;这与一阶逻辑的不可判定性相矛盾 —— 一阶逻辑的不可判定性在 1936 年由图灵呵呵阿伦佐所证明。
在内容上,谢孚和沈有鼎的这些工作属于后来才发展起来的“有穷模型论”领域,有穷模型论起源于经典模型论,但其系统发展归功于复杂性理论的研究。对于自己的这个工作,沈先生在自传中并没有把他列为“主要著作”。
如果一个定义有了正确的形式结构,那么被定义的概念可以认为是明确的,但是还必须加上一个条件,就是用来作定义的那些概念(定义项中所用的那些概念)必须先是明确的。
我们知道,思维对于语言来说,思维是内容,语言则是思维的表现形式。
“逻辑学”就其最广泛的意义讲,乃是和这门那门具体科学都不相同的、以思维的一般形式和一般规律为对象的科学。
我们对范畴或思维的一般内容可以作辩证的处理,也可以作形式的处理。对范畴作辩证的处理时,我们着眼在范畴间的内在联系和互相转化上面,这是辩证逻辑所有的事。对范畴作形式的处理时,我们着眼在范畴间的相对静止的结构关系上面,这是“形式的范畴论”所有的事。
我们甚至可以说,这正是普通逻辑的独特的优点,它使普通逻辑始终不脱离各门学科的具体认识过程,始终和这样的认识过程以及日常思维紧密地联系着。
就是按英国学者的习惯,“形式逻辑”这名词是和“归纳逻辑”对举的,它所指的是以演绎推理的形式结构为重点的,不包括米尔的归纳方法的传统逻辑。而按德国学者的习惯,“形式逻辑”或者是和康德的“超验逻辑”对举的东西,或者是和黑格尔以及马克思主义的“辩证逻辑”对举的东西,至于在这样的传统逻辑里面加进不加进米尔的归纳方法则是一个比较次要的问题。
广泛意义的形式逻辑是包括了归纳方法的。
严格意义的形式逻辑不但要讲究归纳推理的形式结构,它还要研究各种或然性推理的形式结构。
它运用着比日常语言更为精确的符号体系。它把思维过程首先当作演算来处理,然后再加上逻辑的解释,这样分两步走就是数理逻辑的特征。 —— 《光明日报》 1961 年
《逻辑学讲义》第17页,我画了个示意图。
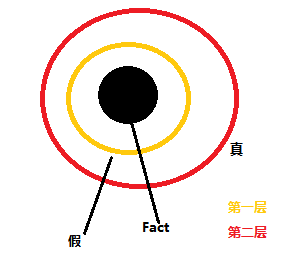
原文是这样的,这是个悖论,Paradox。
(2-1)可以证明我正在讲的可以反驳;
(2-2)可以证明“可以证明我正在讲的可以反驳”;
回到示意图,(2-1)是黄色层,即第一层,是个假命题;(2-2)是红色层,即第二层,是真命题。
摘自 1955 年,美国《符号逻辑杂志》第 20 卷第 2 期。
或作为哲学家有些调皮,作者花了不少笔墨论证了公孙龙这个人重名的几个!事实上,鲁迅先生也论证过人们想象的门神有几个。是一种学术严谨的体现。
但是事实上地面并无任何部分,在任何一瞬,与此轮周面任何部分重合。
彼此根本没有任何接触。
可是实际上,那些逻辑实证论者,他们混淆了“概念”与“名称”。
言合于意的情形叫作“信”,言不合于意乃是说诳。…… 但有时虽言不合于意,凑凑巧与事实符合。
但有时言虽不合于意,凑巧与事实符合。
例如《兼爱中》篇“越国之宝尽在此”就是全称判断。表达全称判断时候用“俱”字。“俱止”指的是某物“不动”。
例如《贵义》篇“贫家而学富家之衣食多用,则速必亡矣”就是必然判断。
例如“见之成见”需要很多条件:人目的视力、光线、对象与人目的适当距离等等。
若是关于某一现象的存在,所作的论证,我的“所以知之故”即我所根据的事实也是某人所已知。
墨者团体中有不少手工业者,每一行的手工业者都有一套代代相传的技术,《墨经》名之为“巧传”。
如果我们仅有一个论题,但没有论据,不能言其“故”,那就是胡说(“妄也”)。《大取》篇以道路喻“理”,“理”正是在论证中指示道路的东西,我们必须遵循它才不至于受困。
有些事物表面上不相似而本质上相同,也有些事物表面上相似而本质上不同。不被表面的现象所迷惑,能透过表象,了然于事物本质上的同异,这就叫做“知类”或“明类”。
“知类”其实就是“明理”,就是辨别不同的本质,也就是认识每一种本质的特殊规律。
知而不争,不可谓忠。
墨家主张兼爱。
“援”是援引对方所说的话来作类比推论的前提。
“援”所用的前提是对方说过的话,或行过的事。
侔式论证,超出这限度,就“转而危”了。侔式推论,己,人也;爱己,爱人也。
至于“爱盗非爱人也,不爱盗非不爱人也”很明显的道理。代表农民利益专门反抗剥削统治者的运动和组织如后来的梁山伯。
侔式推论,否定的前提是正确的,否定的结论则是错误的。
被人强迫犯了罪,责任不在被强迫者身上,所以“为非以人”不是“为非”。注意,至少有两匹马才能说“马或白或非白”。
某人昨日爱人,并不能证明他今日爱人。
《墨经》“一多于五”。
大量笔墨,几乎是这本书结束之前的大论战,就是关于公孙龙此人,到底有几人?
结论是,较早文献所说的公孙龙,是辩者公孙龙。但是《例子·仲尼》、《公孙龙子》给出的形象是晋代人心目中理想的“至人”,刑名家公孙龙。后来受到道家思想的影响。
《周易》主长男用也,故能以阳驭阴,以刚克柔。其序卦也,用构建原则而不用平等原则,是以意味深长。
政界的人大都认为理论是没多大用处的,中国目前所需要的,是踏实的工作。
因为中国文化,同其他文化意义,有它特殊的波动方式。
每一个起伏的大波,在中国文化史里是要战几百年几千年的时间的。
科学与哲学,一定要由刚动的精神才能产生。由静的态度只能产生默悟的玄学,不能产生思辨的哲学。
沈有鼎,逻辑家,1908年生于上海,任中国社会科学院哲学研究所逻辑组研究员。
