例题 14-5 依据已知条件,直线过两个点,可以确定两个位置参数,进而确定曲线方程
例题 14-6 在建立两个微元之间关系时候,需要引入新的微元
例题 14-7 工地打桩,每次打桩,阻力与速度成正比,比例系数K>0,且本次打桩所做的功,与前一次打桩所做的功之比为r。问:如果次数,最多能打进地下多深?
例题 14-8 圆锥形容器,上底半径4CM,水面高8米,容器中的水全部抽出,所做的功。
例题 14-9 洒水车水箱是椭圆形圆柱,装满水,求端面受到压力。
例题 14-10 椭圆钢板浸没于水,短轴垂直于水面,长轴、短轴分别为2a、2b,椭圆钢板所受静压力
两种演算方式:(1)坐标轴建立在下顶点;
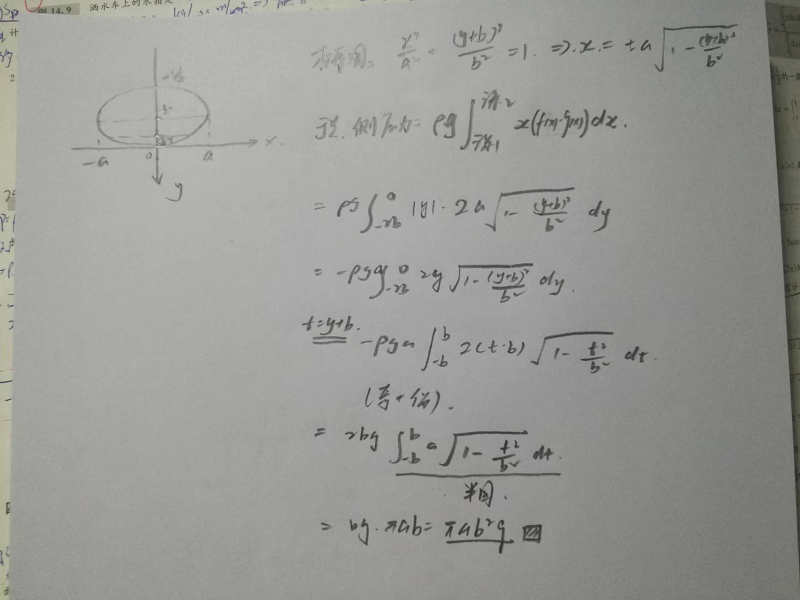
(2)坐标轴建立在上顶点。

例题 14-11 曲线L为 y = x^2/4 - ln(x) / 2, 1<= x <= e 求形心坐标
例题 14-12 曲线 y = ln( 1 - x^2 ), 0<= x <= 1/2 求弧长
例题 14-13 心形线 r = a( 1 + cos(theta) ) 求心形线全部长度
Intermediate
原文链接
长按/扫码,有您的支持,我们会更加努力!


|
