本章节主要是软件工程师考试数据库系统工程师，第三章 数据结构与算法，下篇。

Pre-talk

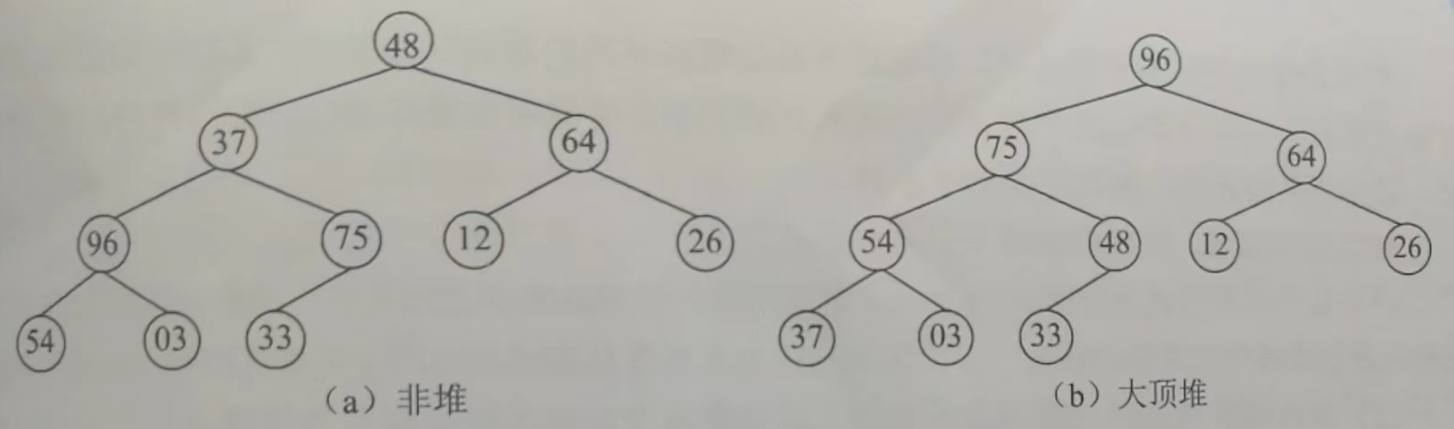
01 排序树

插入排序

void insertSort(int data[], int n )
/*将数组 data[0]~data[n-1]中的 n个整数按非递减有序的方式进行排列*/
{ int i，j;
    int tmp;
        for(i = l;i < n; i++){
        if (data[i] < data[i-1]) {
            tmp = data[i]; datali] = data[i-1];
            for(j= i-1; j>=0 && data[j] > tmp; j--) data[j+1] = data[j];
        data[j+1] = tmp;
        }/* If */
        } /* For */
    }/* insertSort */

冒泡排序

void bubbleSort(int data[],int n )
/*将数组 data[0]~data [n-1]中的 n 个整数按非递减有序的方式进行排列*/
{ int i,j,tag; /*用 tag 表示排序过程中是否交换过元素值*/
    int tmp;
    for(i = 1,tag = l;tag == l&&i < n;i++){
        tag = 0;
        for(j = 0;j             if (data[j]>data[j+1]){
                tmp = data[jl; data[j] = data[j+l]; data[j+1] = tmp;
                tag = 1;
            }/*if*/
        }/*for*/
    }/*bubbleSort*/

简单排序

void selectSort(int data[],int n )
/*将数组 data[o]~data[n-1]中的 n 个整数按非递减有序的方式进行排列*/
{ int i,j,k;
    int tmp;
    for(i =l;i < n;i++){
        k=i;
        for(j = i+1;j <= n;j++) /*找出最小元素的下标,用k表示*/
            if (data[j] < data[k]) k =j;
        if (k != i){
            tmp = data[i]; data[i] = data[k]; data[k] = tmp;
        }/*if*/
    }/*for*/
}/*selectSort*/

快速排序

划分
int partition(int data[],int low,int high)
/*用 data[low]作为枢轴元素 pivot 进行划分*/
/*使得 data[low..i-1]均不大于pivot,data[it1..high]均不小于pivot*/
{ int i，j; int pivot;
    pivot=data[low]; i=low; j=high;
    while(i         while(i < j && data[j] >= pivot) j--;
        data[i] = data[j] /*比枢轴元素小者往前移* /
        while (i < j && data[i] <= pivot) i++;
        data[j] = data[il; /*比枢轴元素大者向后移*/
    }
    data[i] = pivot;
    return i;
}

快速排序
void quickSort(int data[], int low, int high)
/*用快速排序方法对数组元素 data [low..high]作非递减排序*/
{
    if (low < high){
        int loc = partition(data, low, high); /*进行划分*/
        quicksort(data,low,loc-1); /*对前半区进行快速排序* /
        quicksort(data,loc+1,high); /*对后半区进行快速排序*/
    }
}/* quickSort */

关于二叉排序树的音频讲解

02 二叉搜索树

B树

int Bsearch(int r[],int low,int high,int key)
/*元素存储在数组 r[low..high],用折半查找的方法在数组 r 中找值为 key 的元素*/
/*若找到则返回该元素的下标,否则返回-1*/
{ int mid;
    while(low <= high) {
        if (key == r[mid]) return mid;
        else if (key < r[mid]) high = mid-1;
        else low = mid+1;
    }/*while*/ return -1;
}/*Bsearch*/

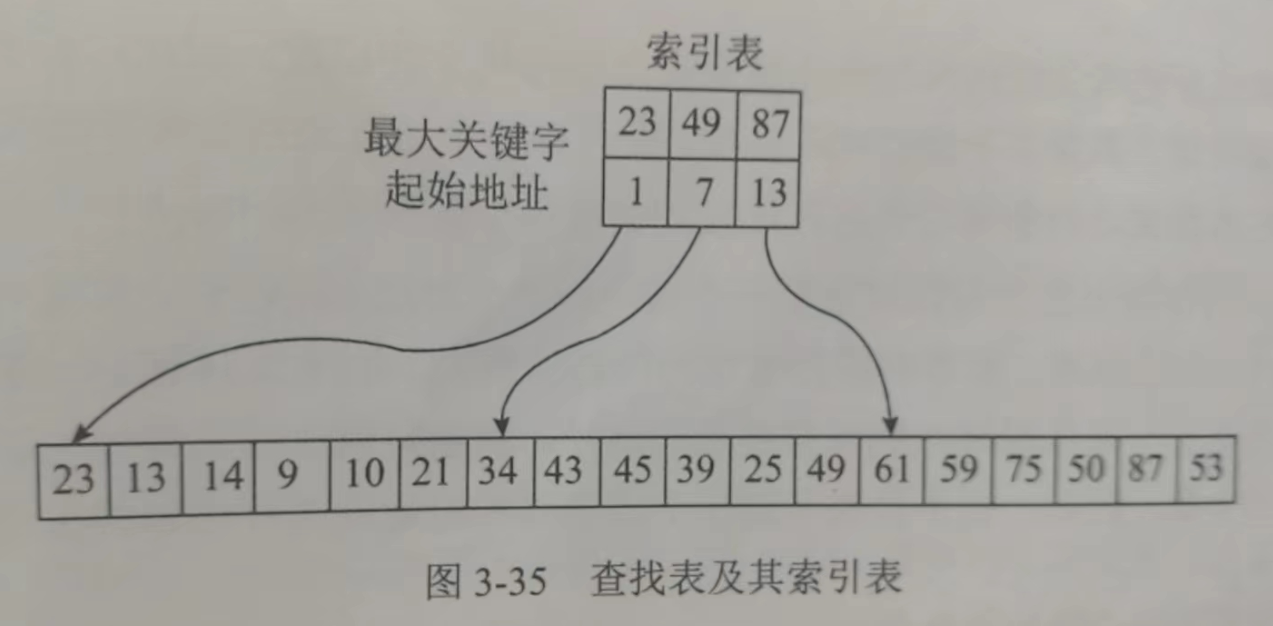
索引顺序查找

树表查找

二叉查找树的查找算法
Bitree searchBST(BiTree root, int key， BiTree *father)
/*在 root 指向根的二叉查找树中查找键值为 key 的结点*/
/*若找到，则返回该结点的指针，否则返回 NULL*/
{ Bitree p = root;
    *father = NULL;
    while (p && p->data!=key)
    {
        *father =p;
        if (key < p->data) p = p->lchild;
        else p = p->rchild;
    }/*while*/
    return p;
}/*searchBST*/

B-树


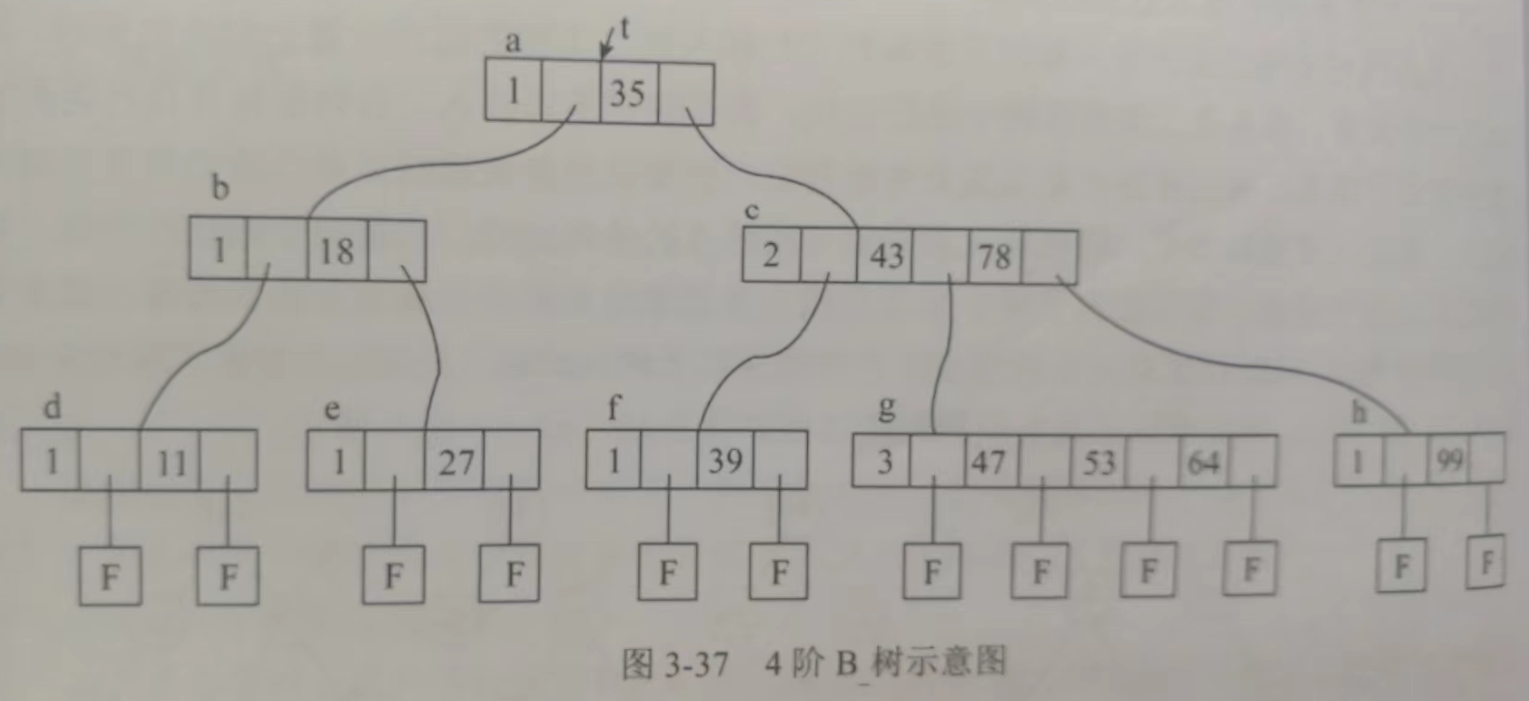
红黑树

哈希查找

(1) 开放定址法

[例3.2] 设关键码序列为 47，34，19，12，52，38，33，57，63，21，哈希表表长为哈希函数为

Hash(key)=key mod 11

用线性探测法解决冲突构造哈希表。
Hash(47) = 47 MOD 11 = 3 Hash(34) = 34 MOD 11 = 1
Hash(19) = 19 MOD 11 = 8 Hash(12) = 12 MOD 11 = 1
Hash(52) = 52 MOD 11 = 8 Hash(38) = 38 MOD 11 = 5
Hash(33) = 33 MOD 11 = 0 Hash(57) = 57 MOD 11 = 2
Hash(63) = 63 MOD 11 = 8 Hash(21) = 21 MOD 11 =10
使用线性探测法解决冲突构造哈希表的过程如下:


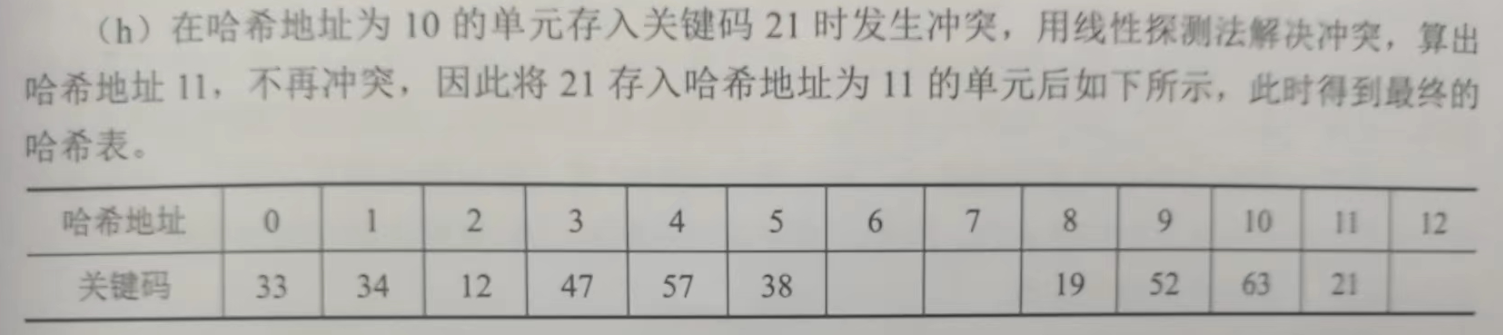
(2) 链地址法

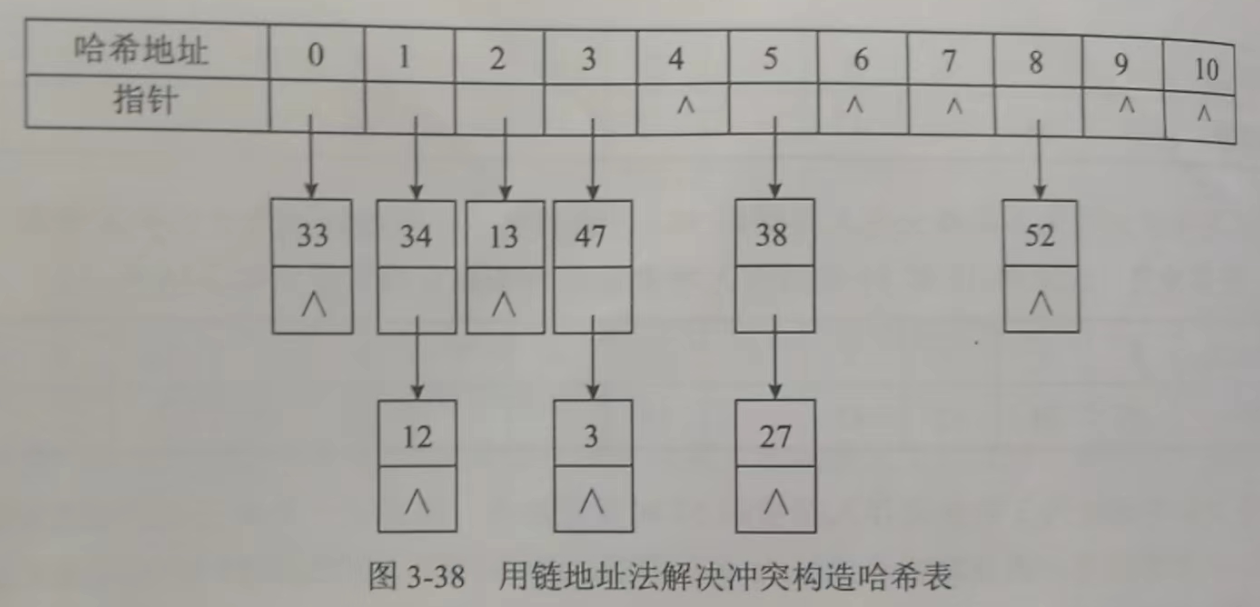
03 递归算法

int Bsearch_rec(int r[],int low,int high,int key)
/*元素存储在数组 r[low..high],用折半查找的方法在数组 r中找值为 key 的元素*/
/*若找到则返回该元素的下标，否则返回-1*/
{ int mid;
    if (low <= high){
        mid = (low+high)/2;
        if (key == r[mid]) return mid;
        else if (key < r[mid]) return Bsearch_2(r，low，mid-1，key);
        else return Bsearch 2(r, mid+1，high， key);
    }/*if*/
    return -1;
} /*Bsearch rec*/

04 图的相关算法

最小生成树

Prim 算法


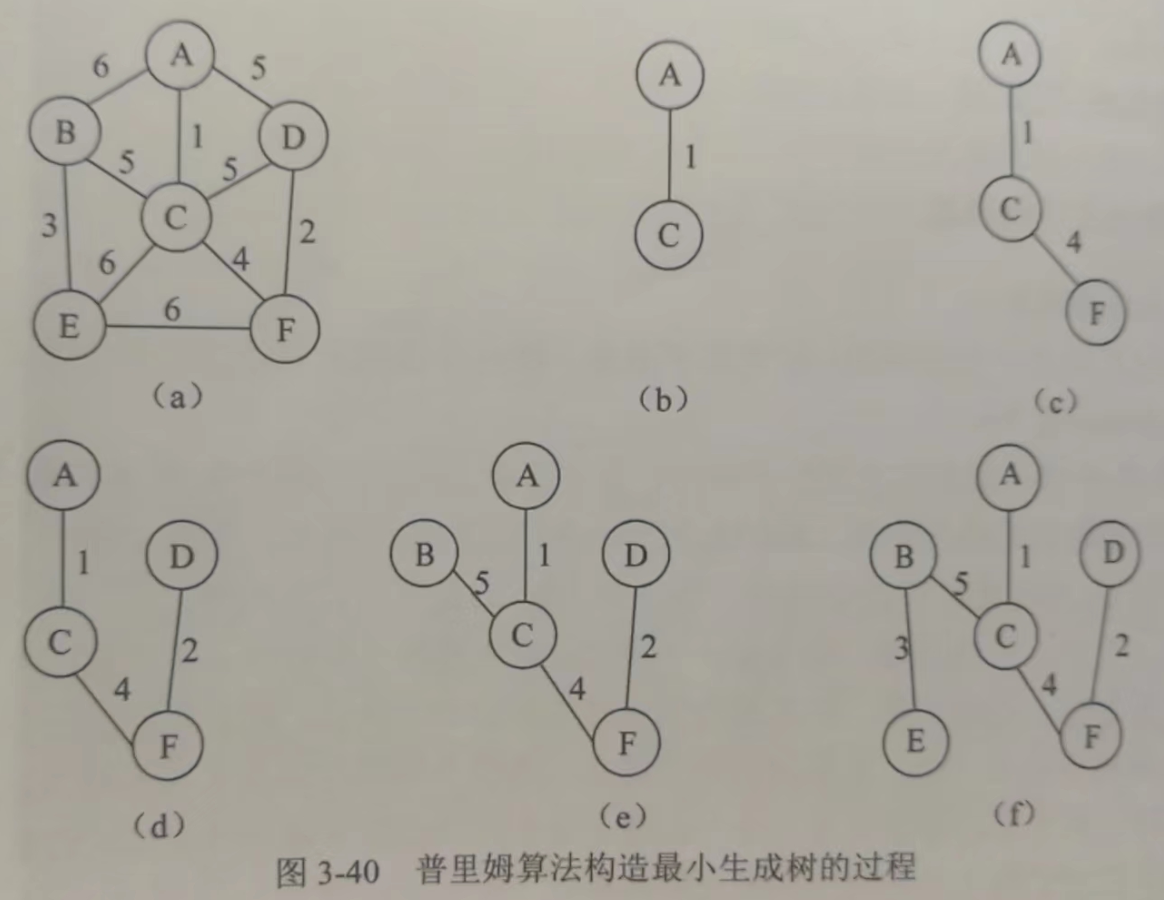
Kruskal 算法

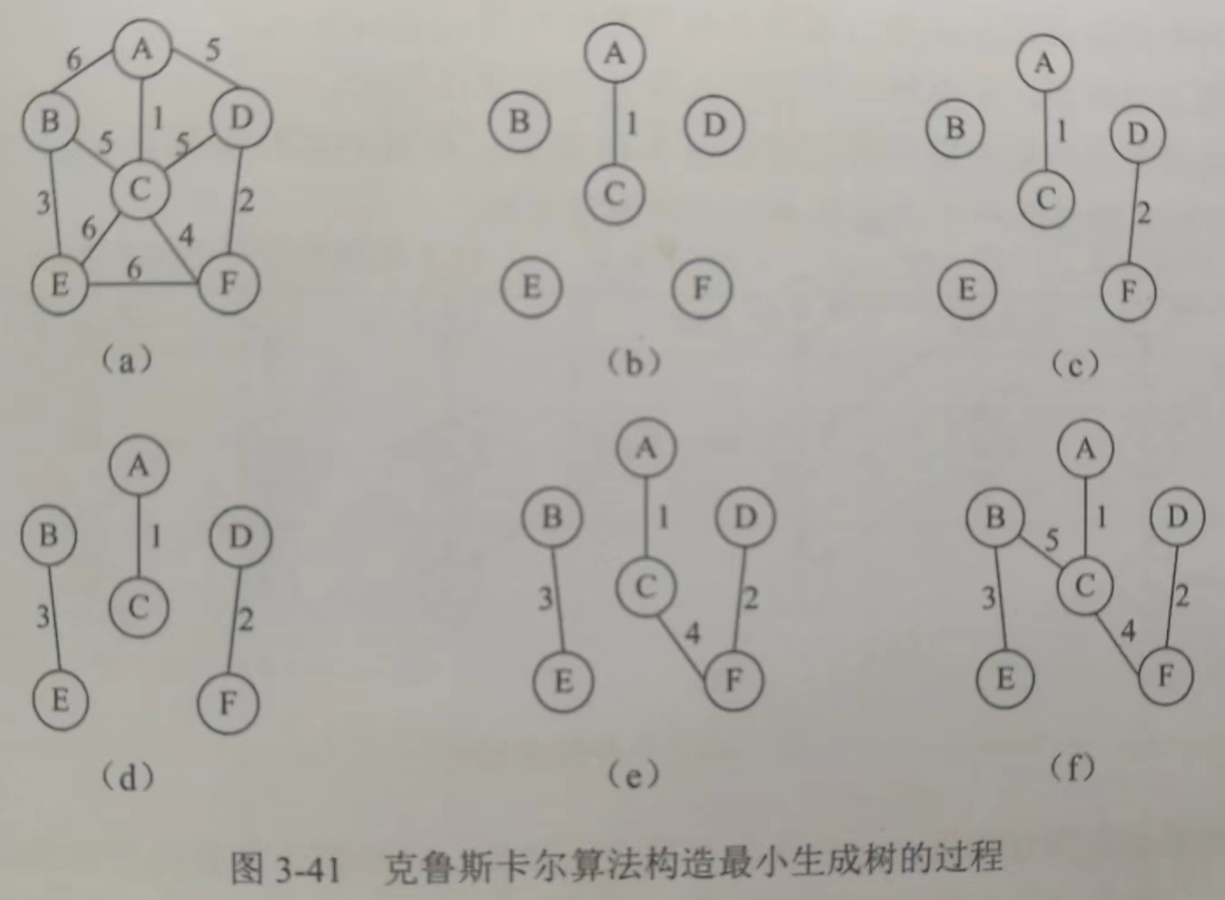
拓补算法

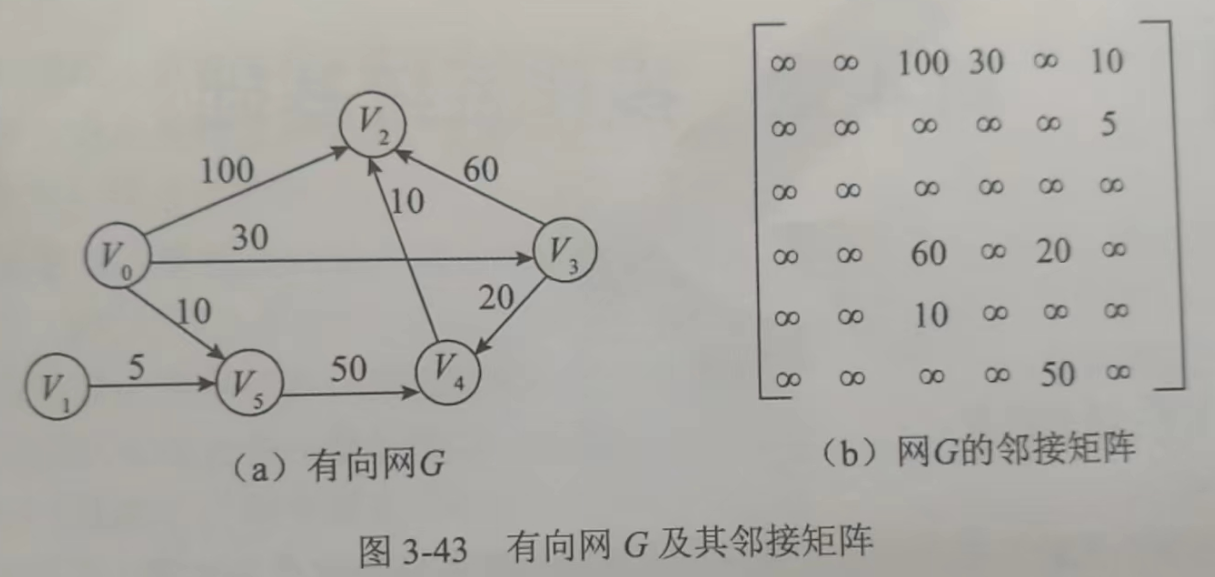
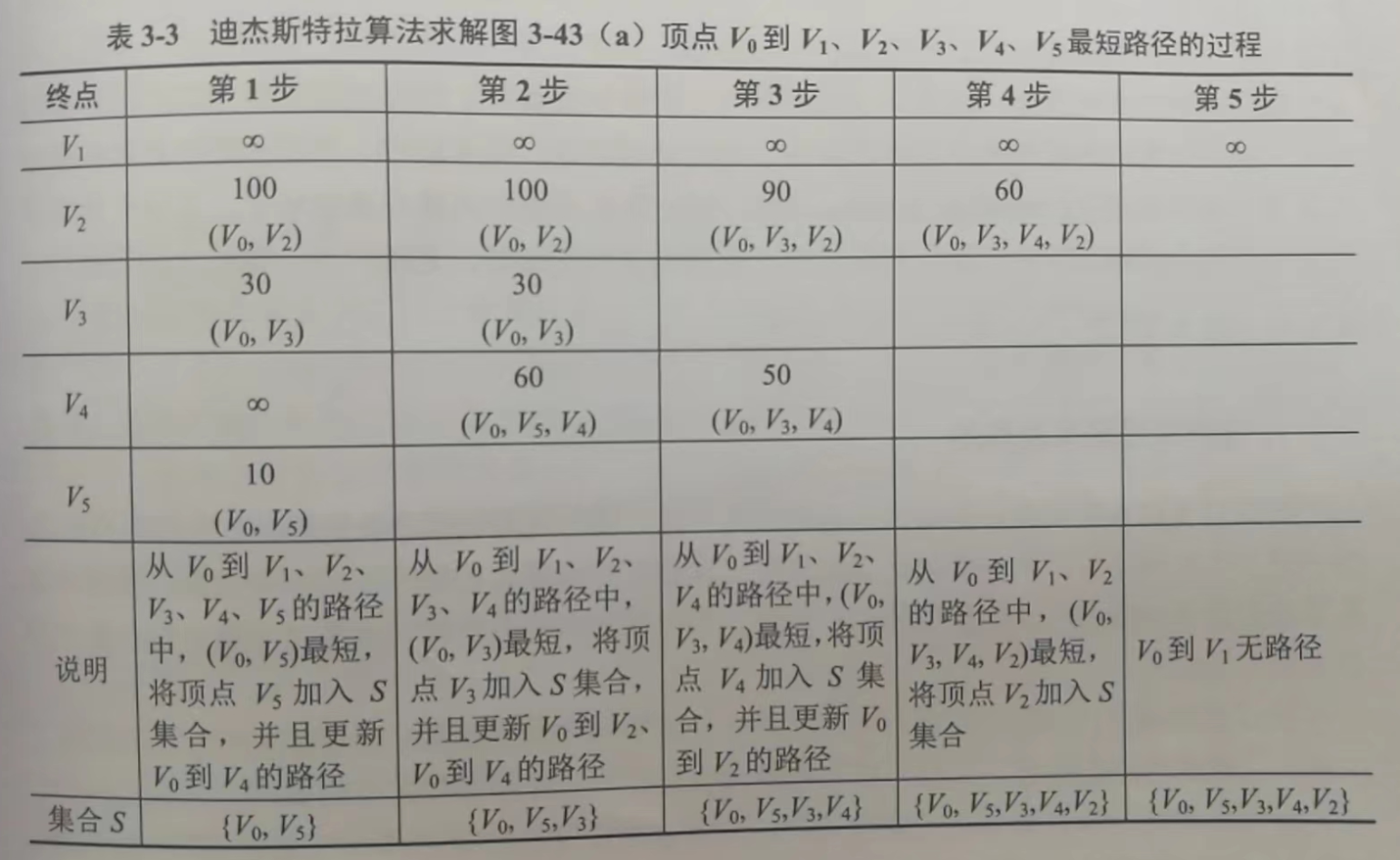
Dijkstra 算法

Ending