原标题:马尔科夫链和隐式马尔科夫链
01 马尔科夫链
马氏链 v.s. 马氏性
任意 n>0,有限或可列个 i 取值,有以下等式成立
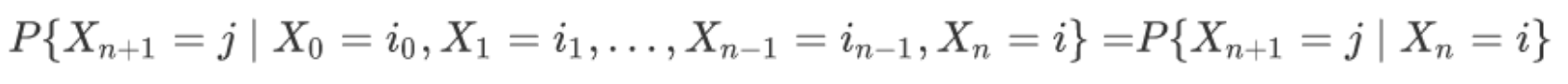
随机过程 {Xn, n=0,1,...} 称为“马氏链”,马氏链的特性,称为“马氏性”。
条件独立
注意,这是本站自行总结的。因为 Jingyi 本身也没有太多同行 Review,如果读者觉得哪里有误,欢迎给我们留言。进一步,我们也会在今后工作中,遇到错误及时纠正的。
如果同时满足 【条件A】 和 【条件B】 才发生的事情,依据马氏性质,可能 i-1 状态是 【条件A】,此时有以下等式成立:
P{事件1 & 事件2 | 条件A} = P{事件1 | 条件A} * P{事件2 | 条件A}
条件独立的变形
注意,这是本站自行总结的。因为 Jingyi 本身也没有太多同行 Review,如果读者觉得哪里有误,欢迎给我们留言。进一步,我们也会在今后工作中,遇到错误及时纠正的。
这个性质告诉我们,如果同时满足 【事件1】 和 【事件2】 同时发生,依据马氏性质,有以下等式成立:
P{事件发生 | 条件A & 条件B} = P{事件发生 | 条件A}
如果 i-1 状态是【条件B】,此时又以下等式成立:
P{事件发生 | 条件A & 条件B} = P{事件发生 | 条件B}
一步转移概率
P{X(n+1)=j | X(n}=i } = p_ij 称为“一步转移概率”。
如果一步转移概率与 n 没关系,则为“时齐马氏链”。
上述 p_ij 组成的矩阵,称为“转移概率矩阵”,注意,每列相加为 1。
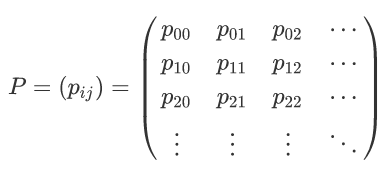
时间不变性
这种只和上一个状态有关的概率,是不随着时间改变的。称为“时间不变性”。
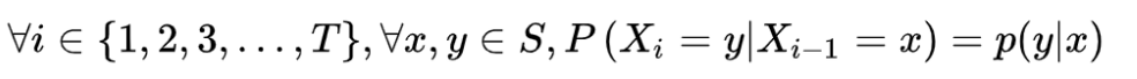
02 隐式马尔科夫链
隐马尔可夫模型(HMM,Hidden Markov Model) : 一种强大的统计工具,通过描述隐藏的马尔可夫链和观测序列之间的关系,其核心组成部分包括
隐藏状态、观测序列、相关的概率分布、概率矩阵。
系统的真实状态(隐藏状态)是不可见的 ,我们只能观察到与这些隐藏状态相关的输出。
如何理解这句话?
依据腾讯云这篇文章《
哈工大学习笔记 | 图文并茂详解隐马尔可夫模型》,我们可以用比较“形象”的感觉,来认知 HMM。
首先,我们先确定,传统的马尔科夫过程,这么来表示:
(S, P_start, A)
状态集合 S,
初始概率 P_start,
状态之间的转移概率 A。
其次,我们再记住,隐式马尔科夫链(HMM),其抽象表达式:
(S, K, P_start, A, B)
状态集合 S,
输出的字符集合 K,
初始状态概率 P_start,
状态转移概率 A,
转移时输出字符的概率 B。
这里从 HMM 参数差异来理解,隐式马尔科夫链是什么,至少,有两个参数会被记录,用于描述“中间输出的字符,及其对应的概率”。
再者,看个案例。
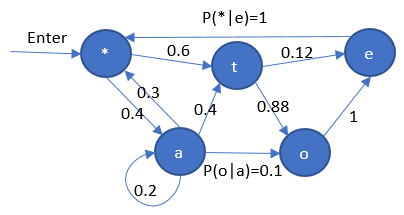
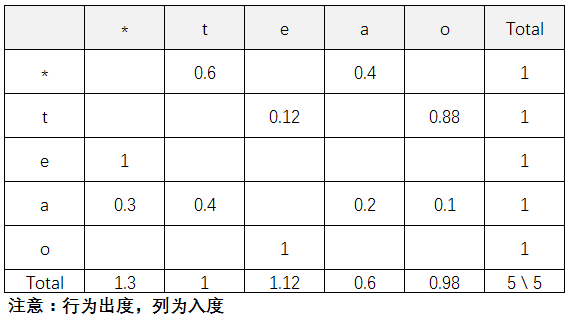
该图可以写成如下的形式:
S = {*, t, e, a, o}
P_start = (1, 0, 0, 0, 0)
上述矩阵,记为 A。
隐马尔可夫模型与马尔可夫模型不同的是各个状态(或者状态转移弧)都有一个输出,但是状态是不可见的。
最简单案例:不同状态,不同输出,输出toe

P{toe}
= 0.6 * 0.88 * 1 = 0.528
增加难度:不同状态,相同输出,输出toe
这里我的理解是,这一步,我们考察从 t->e 路径及其分布。注意,t->e 有好几条路径,案例中选取权重最小的路径。
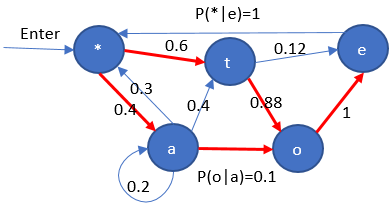
P{toe}
= 0.6 * 0.88 * 1
+ 0.4 * 0.1 * 1 = 0.528
增加难度:不同状态,相同输出,输出toe。但是,a 有一定概率转移到起点,或者 t。
其中第三、第四行的概率,是增加的灵活性,进而形成隐式马尔科夫链。
增加难度:不同状态,相同输出,输出toe。如果,每个点都给到一些概率,使得点转移到其他点。这种概率分布,怎么刻画?
P{toe}
= 0.6 * 0.88 * 1
+ 0.4 * 0.1 * 1
+ 0.4 * 0.2 * 0.3
+ 0.4 * 0.2 * 0.4 = 0.624
HMM: 在状态转移中以特定的概率分布输出
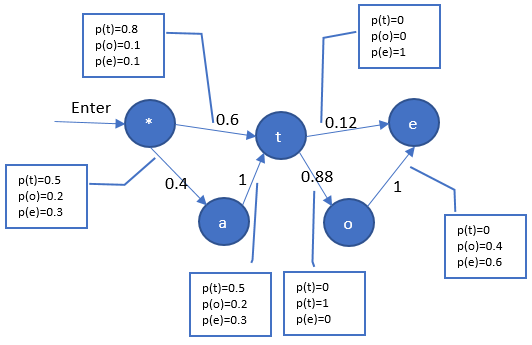
P{toe}
= (0.6*0.8) * (0.88*0.7) * (1*0.6)
+ (0.4*0.5) * (1*1) * (0.88*0.2)
+ (0.4*0.5) * (1*1) * (0.12*1) = 0.237
这个转移到 e 的概率小是因为,过程中以一定概率直接输出,这种输出概率,转移方式,都类似马尔科夫链。这种刻画某种事物的方式,称为“隐式马尔科夫链”。
03 HMM 应用
隐马尔科夫模型的应用,主要聚焦于处理语音和语言问题。对普通的大众来说,语音识别是最直接的 AI 领域之一。从手机软件的语音拨号,到科大讯飞的语音识别系统,再到苹果助理Siri,对话机器人,都或多或少地用到了语音识别的功能。
隐马尔可夫模型,可以分析观察序列得到隐含序列。然而,单纯地使用马尔科夫模型是不对的,我们并不知道马尔科夫模型里的概率,也即一个声音怎么就对应到汉“西湖”,怎么就对应到英文 “Moon River”了?应对这个问题(也称为“痛点”),学者们不打算用一蹴而就的方法,能够
根据一个简单的概率估计 就算出四海皆准的
概率表(即单词之间的映射,是一个概率分布,这部分是 HMM),而是通过大量的数据进行统计并且通过其他方法修正。
数据来源方面,在《数学之美》中讲到,语言学家马库斯认识到建立标准语料库(corpus),并强调该数据库对语言研究的重要性。建立语料库的过程是这样的:从《华尔街日报》中选取一些真实的英语语句,进行词性标注,再加入语法树构建。有了文字语料库,还可以继续添加语音,机器翻译的语料库,供世界上的学者研究。值得一提的是,最近在学习得到听书学习《我看见的世界》,说到斯坦福 AI 科学家李飞飞,她组建并维护了图像数据库 ImageNET。
在上世纪90年代,其核心框架就是用隐马尔科模型对语音的时序进行建模,而用高斯混合模型(GMM)对语音的概率进行建模。而在2006年著名学者辛顿提出深度神经网络(DNN)的模型之后,人们普遍采用了DNN来替换GMM,以提高模型的效果。
参考文献
[1] zenRRan(2019),哈工大学习笔记 | 图文并茂详解隐马尔可夫模型,腾讯网,2019
[2] 北京大学数学系(2024),马氏链,北京大学数学系,2024
[3] stackupdown(2017),隐马尔可夫模型及其典型应用,博客园,2017 