物理竞赛、数学竞赛,就如同马拉松,3 万人参赛,只有 3 个人可以拿奖牌,但是你跑完的时候,你很 明确地知道,自己得到很大的锻炼。
点击购买《
物理竞赛教程 高中第一分册》,还挺受欢迎的一本书。
第七章 机械振动和机械波
| 大标题 |
小标题 |
| 一、简谐振动 |
1.机械振动
2.简谐振动
|
| 二、阻尼振动受迫振动 |
1.阻尼振动
2.受迫振动
3.振动的合成
|
| 三、机械波 |
1.波的形成
2.波的公式
3.波动方程
4.声波
|
| 四、波的特有现象 |
1.波的反射
2.波的折射
3.波的衍射
4.波的干涉
5.多普勒效应
6.驻波
|
从这个章节开始,尝试一些 Acoustic Learning。其实这种修复方法很简单,就是自己给自己讲课,你在讲课过程中,脑子在动、眼睛再看、耳朵在听自己的声音,嘴巴还要发音清楚。是非常锻炼能力的!
关于简谐振动的部分。
2024.8.29 周四
2024.8.30 周五
这里面有个点讲错了。就是加速度 a_M,这个加速度是“径向加速度”,指向圆心。同一个公式中的速度 v_M,是切向速度。
一、简谐振动
1.机械振动
机械振动(简称,振动):物体在某一位置附近沿着直线或弧线,作往复运动。物体回到的位置,称为“平衡位置”。
回复力:使得力回到平衡位置的力,称为“回复力”。

关于回复力和位移的关系,这里要注意,k 未必是弹性系数,只是一个比例系数。

位移与时间 t 关系

角频率的表达式

周期(固有周期)表达式
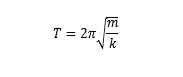
简谐振动的几何表示 —— 换一种理解方式吧!
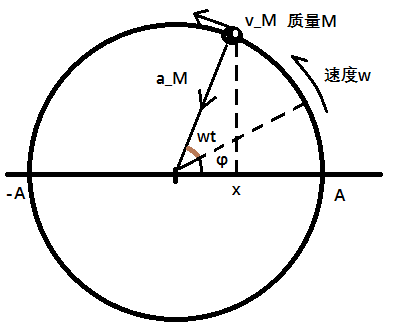
图 1-1
依据上图,一束光自上而下将质点 M 投影在 x 轴上,投影位置的移动,即“简谐振动”。
而在 x 轴上的具体坐标

依据 图1-1 我们感官上理解【切向速度 v】 和 【径向加速度 a】
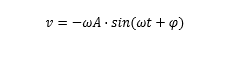
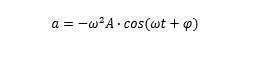
速度和加速度之间的关系

注意到,针对一个简谐振动的系统。系统机械能 = 动能 + (弹性)势能,其中,系统机械能 E,动能 E_k,(弹性)势能 E_p。
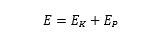
动能表达式

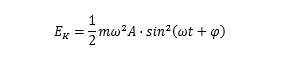
弹性势能表达式
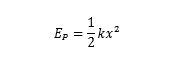
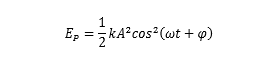
由于弹簧的弹性系数 k = m*v^2

根据上式,我们还能推出角频率表达式
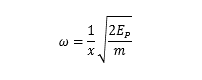
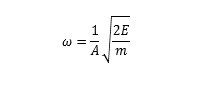
2.简谐振动
这段也是有真人声音的。
二、阻尼振动受迫振动
1.阻尼振动
定义:振幅随着阻力会逐渐减小的简谐振动。
阻力系数 γ,于是阻力表达式
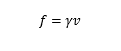
如果阻力系数不大的时候,振动的位移表达式,振动方程

阻尼系数 / 衰减因子 β 表达式
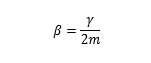
阻尼运动的圆频率表达式,w0 固有圆频率
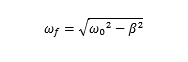
* β< w0,阻尼振动发生;
* β> w0,x 随着时间 t 指数衰减,称为“过阻尼”;
* β= w0,临界阻尼,停留平衡位置时间最短。
2.受迫振动
定义,受到周期外力(驱动力)作用,发生的振动,称为“受迫振动”。
驱动力 f 随着时间正弦变化,表达式
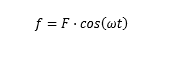
其质点的位移表达式,即振动方程

受迫运动稳定的时候,振动频率为驱动力频率。注意,这个“振动频率”和系统固有频率是无关的,但是振幅和固有频率有关。
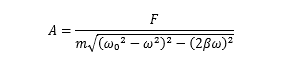
振幅对角频率的偏导为 0 的时候,振幅可以表示成,此时取值最大

如果振幅达到上述表达式,说明达到“共振”。ESP,阻尼系数为 0,角频率为固有频率的时候,振幅 A 趋于无限大。
3.振动的合成
定义,一系列振动的叠加。
(1)同向、同频
合成的振动方程
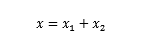

解出振幅 A 的表达式
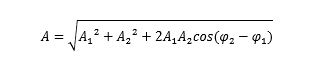
以及 初始相位 的正切表达式
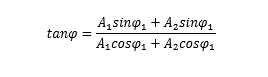
说明:
(a)两个初始相位相等的时候,φ1=φ2,振幅最大,即 A=A1+A2;
(b)两个相位相差 180度,振幅最小,A=|A1-A2|;
(c)取值范围 |A1-A2| <= A <= A1+A2
(2)同向,近似频率
振动方程(位移表达式)
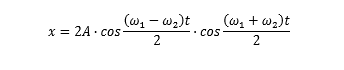
推出,振幅表达式

推出,角频率表达式
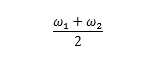
注意,这类振动,称为“拍”。变化的周期,是振动周期的一半。
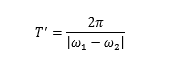
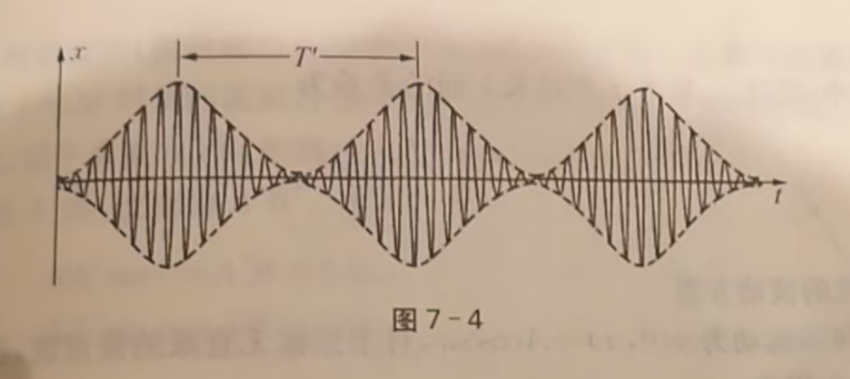
图示意周期变化,这里留个疑问。
(3)垂直向,同频
求表达式的基本思想,即消去 t 之后,求出轨迹方程,其实也是 x, y 表达式。于是,仅含有 x, y 的轨迹方程
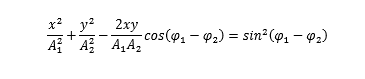
说明:
(a)两个初始相位相。
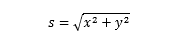
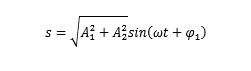
(b)两个初始相位,相差 180 度。
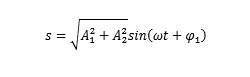
(c)两个初始相位,相差 90 度。
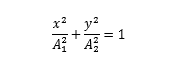
三、机械波
1.波的形成
弹性介质中,质点振动,会对周围产生弹力作用,使之跟着一起振动,“点带点”逐渐在介质中传播开来。称为“机械波”。
2.波的公式
机械波传播过程中,速度、频率、周期的关系
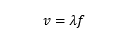
(1)沿着 x 轴正向传播
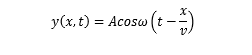
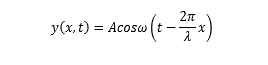
(2)沿着 x 轴负向传播

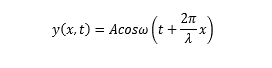
圆波数、角波数(一个波长消耗的相位数量)

3.波动方程
简谐振动的能量守恒,其中,距离 r1有振动 A1,距离 r2 有振动 A2
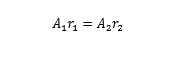
距离 r 振幅 A 球面简谐波动方程
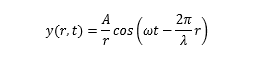
4.声波
声音振动在介质中传播,称为“声波”。声波,是纵波。人耳能听到的,范围 20 - 20000 赫兹之间,超过 2 万赫兹的是超声波,低于 20 赫兹的是次声波。
声强波,单位分贝,范围 0-120 分贝。
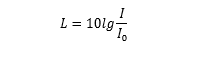
四、波的特有现象
1.波的反射
注意,这边不算特别懂,请读者注重找一些其他资料。

(1)入射角等于反射角;
(2)以振幅 A 为半径作圆 O,质点与 x 轴交点,过交点作圆 O 的切线,这些切线即为机械波的包络面。包络面与 x 轴夹角,两边对称相等。
这里提到的“波面”的概念,书上还是略微模糊。暂时先放一放。
2.波的折射
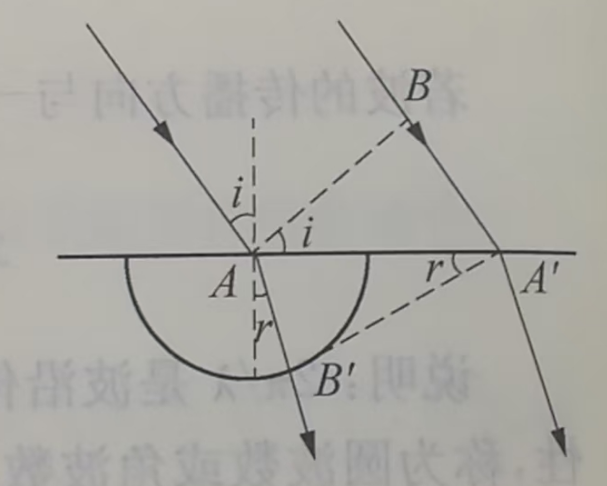
波的入射角怎么确定?
按照上图,我们可以理解为,t 时刻有一个波面,而 t+t_delta 时刻的波面是自己作切线,画出来的。
当我们要求出折射角的时候,t 时刻的波面不变。此时,考虑圆 O 在 x 轴下方的部分(反射角考虑的是 x 轴上方的部分)。如果该波传到 x 轴,交于 A1 点。此时,过点 A1 作圆 O 下方部分切线,通过这种方式,确定折射角。
3.波的衍射
定义,绕过障碍物,沿着原来的方向,继续传播。
4.波的干涉
定义,频率相同,相位差恒定,相互干涉。
(1)相位差 2kPi,合振幅最大,干涉极大;距离 r1, r2 满足

(2)相位差 2kPi + Pi,合振幅最小,干涉极小。距离 r1, r2 满足
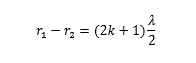
其中,k 属于干涉次级。
5.多普勒效应
定义,观察者在路边观察“动”的波源,观察到的频率,与波源振动频率不一致,称为“多普勒效应”。机械波波速 v,是振动状态相对介质的传播速度。
针对 Receiver 观察到的频率 f_R 有如下表达式
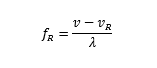
观察到的频率,可以这么表示
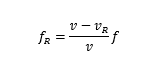
多普勒有一点很重要,移动的 sender 波源,体现在 receiver 看到的波长和频率上。注意,对于波本身而言,是没变的,但是人的感觉变了。
依据速度、频率、波长关系,可以得到 Receiver 看到的波长
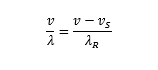
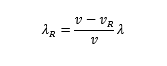
进而达到 Receiver 频率

6.驻波
两个机械波叠加,合成波的方程


振幅表达式
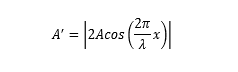
振幅最大,称为“波腹”;振幅最小,称为“波节”。
波腹位置
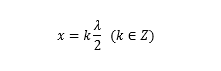
波节位置
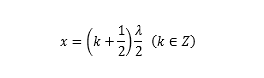
驻波特点:
(1)波形不变;
(2)振幅与 t 无关,与 x 呈现周期变化;
(3)相邻两个波节之间,各点振动相位相同;留个疑问。
