下午分享是小型会议,分别来自香港中文大学、新加坡国立大学、山东大学、上海财经大学、暨南大学,以及清华大学、北京大学的青年学者分别就其研究领域作了报告。
模型一:关于 A/B 原材料的问题
以衣服为例,针对同款衣服可能使用不同的材料,使用 B 材料的时候,能够获得社会效益。几个假设。一是响应变量离散和连续的都要测试和讨论;二是消费者对于 A/B 材料的知晓程度。消费者知道材料有差异吗?消费者知道的情况下,他们能够接受材料有差异吗?三是整个市场上的竞争强度。作者采用的是,赫特林模型,讨论转换成本。
文章的亮点是,针对 A/B 材料的企业,其投资效率作出特别的分析。这个是针对上层建筑报告时候使用的信息。假设某些环保部门,或者致力于环保的企业,他们在考察若干家环保企业时候,如何分配额度,是可以参考的。本次会议由中国运筹协会主办,感兴趣的领导可以给我们写邮件。
模型二:均衡存在性问题
Hyperconvex Space, one of the properties, is nonexpansive absolute retract. 可以简单理解为模长不会 Expand,注意到二维平面里的 convex 距离就会缩短。超凸,距离都不会增加。
其实,接触到这个问题觉得还是比较新颖的,因为很多时候,做出一个结果的时候,这个结果可能带有偶然性,但是你会发现,在工作中很容易就拿来用了。那么,事先证明存在和结果的严谨性,可以使得创业试错成本降低,这是很显然的事情。如果一件事情理论告诉你是不可能的,那么现实中存在的概率会显著降低。这是 Paper work 非常重要的应用。
博弈论中的均衡存在是有条件的。如果,存在性条件不足的话,还有三个臭皮匠,顶个诸葛亮的作用。
一是关于策略的部分,以基金为例。如果一个基金经理,组一个个股和 ETF 的基金,并且计划于 5 年后完全变成 ETF。此时,ETF 的权重,可以认为是个单调策略。所谓决策稳定,即决策函数如果是一个序列,随着 n 增大,该函数序列趋向于一个固定的模式,称为“稳定”。
之前本站阅读过 Competitive & Cooperative Model,上述策略会使得两个参与者(假设只有两个参与者)收敛到 2 个极端。其中,单调策略的存在和完备是可以论证的。
博弈论还能用在电力竞价当中,很多学者将物理中的 Field 和 Algebra 的概念组合起来解释,2-Player Game 的相互竞争价格的问题。
二是策略这件事,就像你过马路的时候,是走人行横道线还是走天桥。针对宽大的马路,非常宽大的马路,一半走人行横道线,一半走天桥,称为“混合策略”。这时候,有什么策略,能使得参与的双方都不改变主意的吗?
正如本站所讨论过的那样,对于 2-Player Game 还是假设双方处于两种状态,一是竞争 ,一是合作;或者“非合作”和“合作”。本篇就认为是两种不同的表述方法。
这篇文章主要部分不算特别理解,在证明某些极限的时候,要注意序列所在的集合的性质,以及该集合能否找到序列去逼近到某个值,或者某种我们想要的场景。
模型三:AI 和人类工种取代性问题
这篇文章很有意思,这位作者论证了,AI 其实是起到一个防火墙的作用。换言之,AI 使得部分人会非常隐匿地提升了自己的工资预期。然而假设也很有意思,略作介绍。如果第 n-1 个人是偷懒的,那么第 n 个人选择努力工作,可能会受损。所以,这个模型偷懒努力的概率是非对称的!换言之,如果带你的人是偷懒的,那么你勤奋的概率,小于 50%。加之,人们看样学样,以及人们会自我鼓励这样的基本假设,得出结论,AI 只是起到防火墙的作用,同时起着降低平均工资,减少不平等这些作用。
诸多文献的结论指向同一个答案,即纳入更多文化,更多风俗,会使得您作出更加明智的决策。
α-core 含义。当一个博弈具有超可加性,那么便只有组成总联盟才能最优化所有博奔者的总得益。作者在介绍文章的时候,讲到 α-core,现在理解核心的含义。
定义,一个支付可转移的联盟型博弈 (N,v) 的核心 C(v) 是一个集合,当中包含所有能满足以下两个条件的支付向量 x=(x1, x2, ..., xi, ..., xn):
(1) x(N) = v(N) # 任何支付向量都属于 C(v) 这个集合。
(2) x(S) >= v(S),任意 S 包含于 N。 # 针对同一个原项,C(v) 是最小的映射。
模型四:路径规划问题
亮点在于,具神智能机器人和环境交互的时候,其实也有一个简短的博弈过程。例如,遇到障碍物要怎么决策?要采取什么 Action?然后环境给到机器人什么反馈?会碰壁?会跌倒?诸如此类。
关键在于,在处理机器人遇到实际障碍,返回一串信息的时候,作者称,可以用大模型解析并形成对话框。
模型五:Agent 能为人类做小组讨论嘛?
这位是清华学者胡老师做的工作。分享了人工智能组和人类组在三种情形下的讨论结果是否有差异,事实上,有一些很有意思的结论,大家有兴趣可以搜论文,关键词 Foreign Policy Decision,Randomized Controlled Experiments, Multi-Agent。
LLMs 有点是知识多不疲倦,缺点是会有系统偏差。笔者认为,主要是算法是 measurable,会有系统偏差。那么,到底是 LLMs 偏见大还是人类偏见大呢?这也是很大的议题。
其他例如山大的学者徐老师讨论资本化还是商品化的问题也有非常有意思的结论。
商品化,《资本论》关于商品化定义,商品的定义、商品交换过程,货币与商品流通。商品化的意思就是,一样东西一旦用于交易,它就被商品化了。
资本化,会计上的定义。资本化,是指企业的某一项支出,不能当做费用一次性计入当期损益,而应该当做某一项资产长期的支出,计入该长期资产的成本,并在以后的会计年度通过逐渐折旧或摊销的形式分批进入成本费用,并通过销售产品收取款项的形式获得补偿。
知乎上某 CFO 解释,资本化支出就是你为了获得某项长期资产所付出的必要开支,这种支出必须作为产品成本的一部分,影响的是资产负债表科目(固定资产、无形资产、在建工程等)。
说明,资本化是一次支出大额,但是在以后年度摊销一种钱货交换的模式。和商品化不一样的地方在于,商品化每个轮次都是钱货两清。
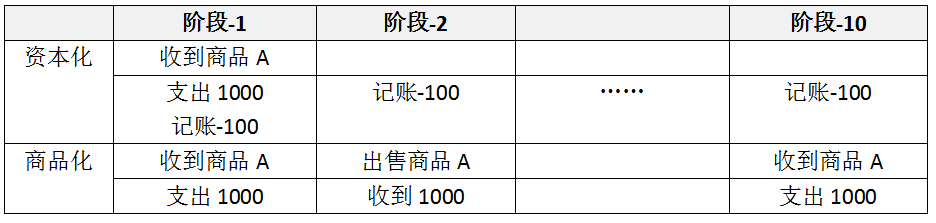
无限期博弈怎么处理?测试某策略,好则继续,坏则停止。直到收敛到某个固定策略,有时候会局部收敛。注意,某些人会犯的错误,期待一次决策就直接获益。
市场距离,可以用相关性,或者相似程度,或者其他度量距离的方式,来处理一系列多维度的刻画。这个概念,能说明什么?说明,市场距离越小,分享信息的效果越好。
最后讨论了资本化和商品化和社会福利的关系。这是一个比较有意思的角度。
关于 Hotelling Model
Hotelling/霍特林模型,“考虑空间差异的,用来解释企业选址和定价的产品决策模型”。考虑三种 Hotelling Model,选址、定价、选址后定价模型。
第一,仅选址。
这个模型的均衡收敛在 1/2,经典模型了,大家都查得到。
第二,仅定价模型。
一座城市分布 [0,1] 上,此时,t 是时间,x 是坐标,p1 到企业1成本,p2 到企业2成本。如果交通成本是线性函数,则有。
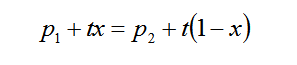
如果交通成本是二次函数,则有。
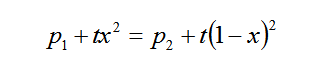
这里,解出 x 和 1-x 之后,就是企业1需求和企业2需求。如果定义成本 c 是一致的,那么他们的利润函数为
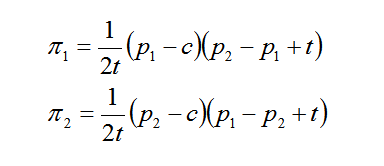
对上述两个式子,分别对 p1,p2 进行求导并等于 0。联立之后可以解出解析解,求出的 x,其实是“无差异点”。
第三,选址后定价。
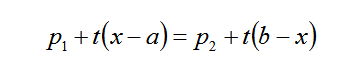
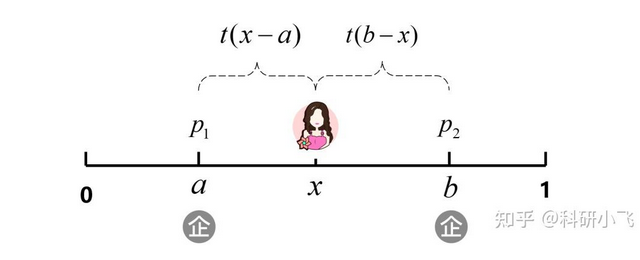
注意到示意图,分为三个区域。区域一[0,a],属于只会买企业1的用户;区域二 [a,b],需要讨论的区域;区域三 [b,1],属于只会买企业2的用户。
解出模型三的最优价格。
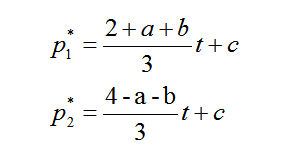
将最优的价格代回到利润函数,得出
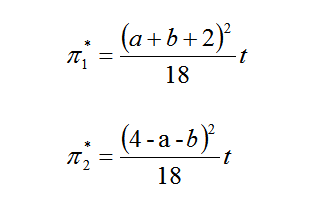
对 a 和 b 求导,得到以下结论。
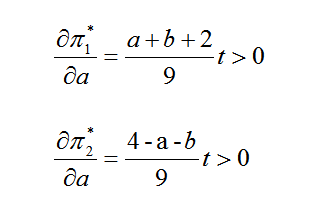
这个式子用动态分析,点击阅读原文《
Hotelling霍特林模型(上) | 3种模型求解及Maltab代码——基于一次交通成本》。
由动态分析结果,一定会平分市场,最终求得 a=b=0.5。
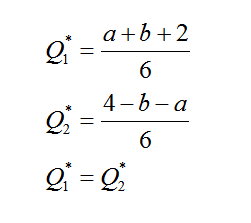
最后,两个选址收敛到中点位置,具体参数如下:
最优价格 p1 = p2 = t+c;
最优份额 Q1 = Q2 = 1/2;
最优利润 Profit1 = Profit2 = t/2。
至此,2025 年 8 月 26 日的会议整理完毕,这是本人第二天整理的结果。
参考文献
[1] 姜少峰(2025),博弈论基础,北京大学前沿计算研究中心,2025
[2] 该用户已注册(2022),静态合作博弈--核心与稳定集,知乎,2022
[3] 科研小飞(2023),Hotelling霍特林模型(上) | 3种模型求解及Maltab代码——基于一次交通成本,知乎,2023
[4] 庄生梦蝶(2020),如何理解费用满足资本化条件和不满足资本化条件?,知乎,2020
[5] 东奥初级会计职称(2025),什么叫资本化和费用化,东奥会计在线,2025
[6] 不正经的政经(2024),《资本论》13 商品化的定义,作用和意义,知乎,2024
