01 Support Vector Machine SVM基本思想

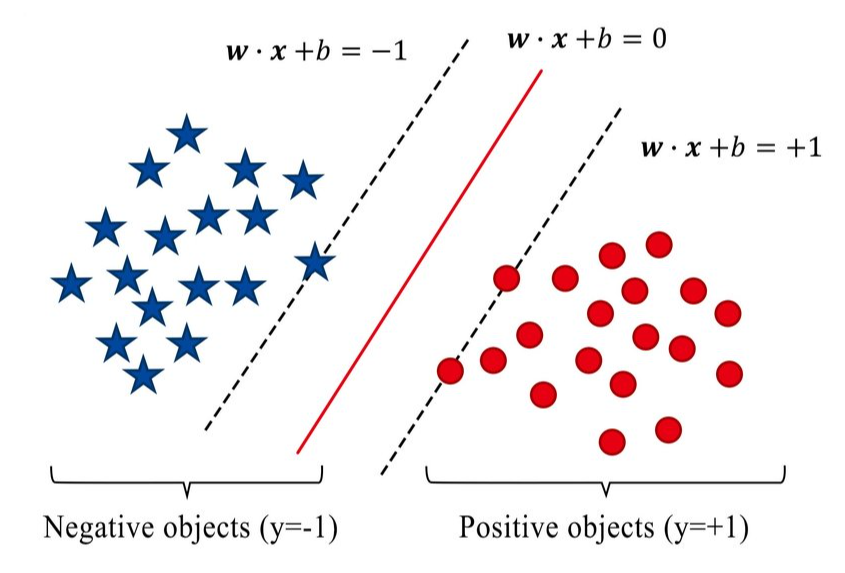
基本思想是找到一个超平面，分割数据集。

先导知识：Ax + By + Cz + D = 0 是一个平面方程，如何确定这个平面长什么样子？ 即确定 A, B, C, D。在本文中，A, B, C 写成 w(i)。

最优化问题

Min 0.5 * |w|^2

s.t. Y(i) * ( w.T * x + b ) >= 1 ; (i=1,2,...,m)

此为 SVM 基本问题。

02 Dual Problem

Max ∑α(i) - 0.5 * ∑∑α(i)α(j)Y(i)Y(j)x(i).T * x(j) ; (i=1,2,...,m)

s.t. ∑α(i)Y(i) = 0

此为对偶问题。

03 Sequential Minimal Optimization SMO

1. 确定 α(i) 和 α(j) 代入上述 Object 和 Subject 两个等式，可得出一个满足 KKT 条件，另一个不满足；

2. 两两 Search ，直至发现 KKT 条件违背了之后，对目标函数影响最大的 α(i)；

3. 挑出的向量，则为 Support Vetor 。

04 KKT 条件

满足方程组：

1. α(i)>=0

2. Y(i) * f[x(i)] - 1 >= 0

3. α(i) * ( Y(i) * f[x(i)] -1 ) = 0

05 核函数

基本思想，低维度线性不可分情况下，找到 核函数 使得其线性可分。这里的线性可分是高维度线性可分，但无需知道如何映射到高维度或者高维度空间的具体形态。

Kernal: K(x(i), x(j)) = = phy(x(i)).T phy(x(j))

phy() 是低维度向高维度的应映射。

原问题

Min 0.5 * |w|^2

s.t. Y(i) * ( w.T * phy(x(i)) + b ) >= 1; (i=1,2,...,m)

对偶问题

Max ∑α(i) - 0.5 * ∑∑α(i)α(i)Y(i)Y(j)phy(x(i)).T * phy(x(j))

s.t. ∑α(i)*Y(i) = 0

06 软间隔

原问题

Min 0.5 * |w|^2 + C∑e(i)

s.t. Y(i) * (w.T * x(i) + b) >= 1-e(i)

e(i)>=0; i=1,2,...,m

此为“软间隔支持向量机”。

对偶问题

Max ∑α(i) - 0.5 * ∑∑α(i)α(j)Y(i)Y(j) x(i).T * x(j)

s.t. ∑α(i)Y(i) = 0

0 <= α(i) <= C ; i = 1,2,...,m

KKT条件

1. α(i) >= 0, u(i) >= 0

2. Y(i) * f[x(i)] - 1 + e(i) >= 0

3. α(i) * ( Y(i) * f[x(i)] - 1 + e(i) ) = 0

4. e(i) >= 0, u(i)e(i) = 0

多出的几个条件，是加上的 Slack Variable。

07 Support Vector Regression SVR

原问题

Min 0.5 * |w|^2 + C ∑(e_hat(i) + e(i))

  s.t. f[x(i)] - Y(i) <= r + e(i)

  Y(i) - f[x(i)] <= r + e_het(i)

  e_hat(i) >=0, e >= 0; i=1,2,...,m

对偶问题

Max ∑Y(i)*(α_hat(i) -α(i)) - r(α_hat(i) + α(i))

  - 0.5*∑∑(α_hat(i)-α(i))(α_hat(j)-α(j))x(i).T * x(j)

s.t. ∑(α_hat(i) - α(i))=0

0 <= α(i), α_hat(i) <= C

KKT 条件

1. α(i) * (f[x(i)] - Y(i) - r- e(i)) = 0

2. α_hat(i) * (Y(i) - f[x(i)] - r - e_hat(i)) = 0

3. α(i)α_hat(i) = 0, e(i)e_hat(i) = 0

4. (C-α(i)) * e(i) = 0, (C-α_hat(i)) * e_hat(i) = 0

截距的求法

b = Y(i) + r - ∑(α_hat(i) - α(i))x(i).T * x(j)

08 核方法

LDA 公式

Max J(w) = w.T * S_b * w / w.T * S_w * w

u(i) = ∑phy(x) / m(i)

S_b = (u(1)-u(0)) * (u(1)-u(0)).T

S_w = ∑∑(phy(x)-u(i)) * (phy(x)-u(i)).T

KLDA 公式

u_hat(0) = K * ones(0) / m(0)

u_hat(1) = K * ones(1) / m(1)

M = (u_hat(0)-u_hat(1)) * (u_hat(0)-u_hat(1)).T

N = K*K.T - ∑m(i)u_hat(i)u_hat(i).T

Max J(α) = α.T * M * α / (α.T * N * α)

09 朗读